The last two weeks have seen heated debate about a mathematical puzzle posed by Gary Foshee and reported by New Scientist (discussions here and here and here).
Gary Foshee, a collector and designer of puzzles from Issaquah near Seattle walked to the lectern to present his talk. It consisted of the following three sentences: “I have two children. One is a boy born on a Tuesday. What is the probability I have two boys?”
“The first thing you think is ‘What has Tuesday got to do with it?'” said Foshee, deadpan. “Well, it has everything to do with it.” And then he stepped down from the stage.
This is the answer: 13/27.
Many people will intuitively say that the answer is 1/2 (=the chance of having a boy or a girl), but probability aficionados will give the answer 1/3, since this is the Boy or Girl Paradox: We are not told that the speaker has a child and is waiting for another, but that he already has two children. Two children can come in four configurations: 1) boy/girl, 2) girl/boy, 3) girl/girl, 4) boy/boy. Since he has one boy, we are looking at the options 1, 2, or 4. Only the boy/boy combination includes two boys, so the probability is 1/3. In other words, order matters and completely changes probability.
So what has being born on a Tuesday got to do with it? Why would the answer not still be 1/3? The New Scientist has a good explanation toward the bottom of the article. Simply count the different combinations of genders and weekdays, which gives the result (number of combinations with two boys, at least one of which was born on a Tuesday) / (number of combinations with at least one boy born on a Tuesday). The result really is 13/27.
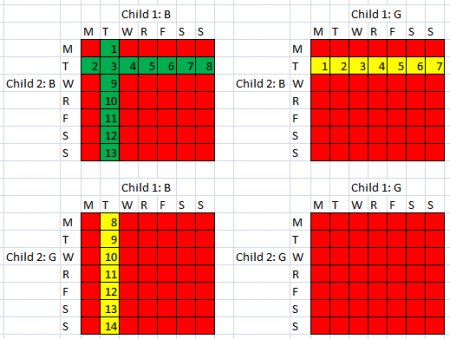
This is the best illustration I have found: This shows all the boy/girl pairs as well as the possible weekdays on which they could be born. Green represents situations with two boys, at least one of which was born on a Tuesday. Yellow represents at least one boy born on a Tuesday. Red is neither. Hence the answer is green/(green+yellow)= 13/(13+14) = 13/27.
But again, what has Tuesday got to do with it?
More below.
Discussion
It is an appealing puzzle because even once you (or at least I) accept the 13/27 calculation and visualize it, it still is wildly counter-intuitive that being born on a Tuesday influences the probability of having a brother. (Actually it doesn’t – see below.) What’s also strange is that with a rarer trait (say, being born on February 29), the probability of having two boys approaches 1/2. (For a trait with probability 1/A, the probability of having two boys is 2A-1/4A-1.)
Other people with more skill in probability theory have explained it well (search for “cocktail party” here), but I thought about it moving backwards from the result: Our intuition (which is correct) is that boys born on Tuesdays do not have a larger chance of having a brother than boys born on other days. Therefore the 13/27 result seems absurd because we could repeat it with all days of the week, add up the results, and reach the conclusion that the answer to the boy or girl paradox was 13/27 and not 1/3. And that is the hint: We are not really calculating what we think we are calculating.
It is really a question of formulation. The puzzle is not “My firstborn is a boy born on Tuesday” or “I have exactly one boy born on a Tuesday”, but “One [or more] is a boy born on a Tuesday [but I am not telling you which one].” Which means that we did not calculate whether being born on a Tuesday influences the probability of having a brother.
As I stated above, the absurdity comes from the fact that we might imagine that we had sliced the possibility space (2 genders, 7 weekdays) into 7 equally big slices, but did we? Try repeating the calculation for “boy born on a Tuesday”, “boy born on a Wednesday” etc…
Now consider the case of the oldest child being a boy born on a Tuesday, and the youngest child being a boy born on a Wednesday. This will count toward both the probability of “two boys when at least one child is a boy born on a Tuesday” and “two boys when at least one child is a boy born on a Wednesday”. Many cases are counted for several weekdays. This is why the probability goes up from the expected 1/3, approaching 1/2.
Why this is such a good puzzle:
- It is a puzzle within a puzzle.
- Like the Boy or Girl Paradox, which encourages us to answer from the knowledge that the boy/girl probability is (roughly) 50%, this puzzle encourages us to answer from the knowledge that being born on a given weekday generally doesn’t influence other probabilities. In both cases, that is not what the puzzle is actually asking us. We are tricked into using a stock answer that is not appropriate for the given puzzle.
- It appeals to puzzle and probability theory fans by building on an existing puzzle.
- It gives a result (approaching 1/2) which is exactly the result that connoisseurs know should not be the answer.
- It uses a counting technique specifically designed to prevent from counting the same case twice, and we may be thinking that “at least I am not counting anything twice”, but that is exactly what we are doing.
- The very terse explanation of the puzzle is deliberately misleading. When Foshee says ‘One is a boy born on a Tuesday. … What has Tuesday got to do with it? Well, it has everything to do with it.“, it makes it sound like we are doing a probability calculation depending on one particular boy, when in fact we are doing a calculation depending on “one or more children being a boy born on a Tuesday” – hence we end up counting some combinations for several weekdays.

@Jesper: I never said the differences between the “official” results and mine were due to mixing up prior and posterior probability. That mix up is a failure to recognize the application of a condition. The difference between our results is due to which system is used to define that condition. It is related to the Principle of Restricted Choice in bridge: you need to know not just what the end result is, but how it was arrived at when others might have been arrived at as well.
And the ambiguity comes because the “given” information is about the family, not the manner in which the information came to be “given” to you. The difference between the two forms you described is that the first is unambiguously 1/2, while the second is still ambiguous: both 1/2 and 1/3 are possible. In the first, it is clear that the gender is observed information. You want the second to mean that the gender “boy” was required – that only qualifying fathers were considered. But the actual meaning of what you wrote can be either: observed, or required. To accomplish what you want, you need to say “Given that a man is chosen from all men who have two boys and at least one boy.” This is different because the “given” information is about the manner in which you obtained the information, not the family in the example.
As I hope I conveyed to you above, anything that merely describes one family as a posterior event is an observation. Your cocktail party comparisons described the method, so they got around this problem. So simplify them:
Cocktail party game played in room #1. All fathers of two are asked to raise their hand. 100 do. They are asked to tell a neighbor about one child. Then, neighbors who were told about a boy are asked to raise their hand. 50 do.
Cocktail party game played in room #2. All fathers of two are asked to raise their hand. 100 do. All of them who don’t have a boy are asked to lower their hands; 75 remain up.
Later, it is *given* to you that Gary Foshee was identified as “someone with two children has at least one boy” at the party. Which room was he in? You can’t tell, so your second form is still ambiguous. (And I disagree with Devlin, that the word “given” changed anything. All it means is that you don’t question the fact, while he is assuming it addresses how you got the fact. And you seem to be uassuming the same thing. This is a digression, but it is why I emphasized the word “if” before, and put “given” is quotes here.)
As you described with the cocktail party examples, the way you get 1/3 is to make “boy” be required information about any father you select, while “Tuesday” is observed after you select him. Regardless of how you want to interpret the form of these questions AS THEY WERE ASKED BY FOSHEE, you can’t do it differently for the two kinds of information. Either “Tuesday Boy” is all required, or all observed. So 1/3, for the Tuesday problem, cannot be right.
The reason the 13/27 answer (and other, different answers as you change the added condition) is unintuitive, is because the “required” interpretation for “given that he tells you he has one child that belongs to ” is itself unintuitive. But for some reason that is harder to see when the “specific subset” represents half the population, like “boy.” (I think the reason is that the statement sounds like an observation. But since “girl” and “not boy” are the same thing, it disguises the need to observe “girl.” But again, I digress.)
@ron
“A two child family has at least one boy. He is born in a period of the calendar called “a day”. What is the probability that his sibling is a brother?”
Your problem statement is a little ambiguous.
“A two child family. Picking a random one … he is a boy. What is the probability that his sibling is a brother?” = 1/2
“A two child family has at least one boy. What is the probability that there are two boys?” = 1/3
“A two child family has at least one boy born in a period of the calendar called “a day”. What is the probability that there are two boys?” = 1/3
This last one is because ‘ born in a period of the calendar called “a day”’ is true for all possible combinations. (Try simulating it on a computer).
Again, see the cocktail party explanation. Focusing on Tuesday does not increase the likelihood of having two boys, it just means that several boy-boy combinations will get counted twice, giving the illusion that the likelihood of having two boys has been increased.
@JeffJo
Ah, I think I read your comment a little too quickly. We completely agree that it all comes down to how we interpret the question, and that how we obtained the information is important. The link that Devlin provided to the discussion of Word Problems in mathematics was also pretty interesting.
As I was also alluding to above, the interpretation of Foshee’s puzzle is very clear if you are reading it as belonging to the math puzzle genre (which I did).
If we are not reading it within that genre, it can be hard to distinguish whether the result is counter-intuitive because we are interpreting it using (ambiguous) everyday language or because we don’t understand probability. A little bit of both, perhaps.
@Jesper: yes, we do seem to be in agreement, except about how to express the simple question whose answer is unambiguously 1/3. I say it has to describe what happens with GG families, and not just ignore them because Foshee’s isn’t one of them. Even is a “mathe puzzle genre.” You seemed to agree with Devlin that saying “given” changed something, and I have no idea what that is. I am a mathematician, so I do know what “given” means to Devlin – it just doesn’t get him where he thinks.
There is no such thing as “the math puzzle genre,” that is a rationalization used to cover an assumption that is incorrect. Specifically, if you do the exact same thing with the Monty Hall problem, you get 1/2 for it. That “same thing” is creating an isomorphism where the sample space is every event that is consistent with what you learned about the example, ignoring how that knowledge came to you. So the sample space is {BB, BG, GB} or {Car@1, Car@2}, respectively, since that is what you learned. Each set is equiprobable since it is equiprobable without the knowledge. You ignore that the father had to choose in the BG or GB cases, and that the host had to choose in the Car@1 case. So your “math puzzle genre” is saying the probabilities for the MHP are 1/2 for each door. No “math puzzle solver” will agree with that, so that cannot be the “genre.”
@Ron, try this problem:
Say Foshee says to you “A bowl has red, green, blue, and yellow M&Ms in equal numbers. I take two, and one of them is green. What is the probability I got two green M&Ms?”
Using the terminolgy I used before, the answer based on the “observed” assumption is 1/4. That means that Foshee was free to name any color from the one or two he actually got, and he chose green. The “required” answer is 1/7. That means that Foshee could only mention green – if he didn’t get one, he would have to put the M&Ms back back just like you “reflipped” the two coins in your simile.
I don’t know about you, but from that statement, I’d assume that Foshee picked randomly and observed that one was green, rather than assume he would’ve put some back and tried again.
Now, change the problem so that half of each color are actually peanut M&Ms, and half regular. Suppose Foshee tells you he got one green peanut M&M and asked the same thing. Which answer would you accept:
1) “Observe” both color and kind: 1/4.
2) “Observe” color but “require” peanut (putting back if no peanuts): 1/3
3) “Require” green (putting back if no green) but “observe” kind: 1/7
4) “Require” both green and peanut (putting back if no green peanuts): 1/5
#1 is my answer, the equivalent of 1/2 for all of the two-boy questions. #2 is Foshee’s answer, the equivalent of 13/27. One of #2 or #3 is the equivalent of your answer, but it isn’t clear which. Is the statement “initially” about a green M&M, with a condition that it has a peanut? Or is it “initially” about a peanut M&M, with the condition that it is green? Until you define how and why those terms apply, I can’t say.
Jesper @ July 6th 9.50, you said:-
“Focusing on Tuesday does not increase the likelihood of having two boys, it just means that several boy-boy combinations will get counted twice, giving the illusion that the likelihood of having two boys has been increased.”
We are in total agreement on this point. So my question to you (and the assembled might of probability experts in the academic and corporate worlds), is:-
“What is the consistent calculation and counting method which both answers the “simple” question correctly AND makes it mathematically clear that the likelihood of having two boys does not increase when you focus on Tuesday?”
I think you would agree that such a method would carry more integrity than one which produces an illusion.
Ron: the method you ask for is the one that gives 1/2 as the answer to both. I’ve tried to tell you this several times, but you keep insisting on holding on to the 1/3 solution and then forcing the Tuesday answer to match it.
It is a difference in interpretation that leads to 1/2 vs. 1/3, and you are mixing the two modes of interpretation together in an illogical fashion.
Foshee’s method equates “the family has at least one boy” with “the father says the family has at least one boy.” It corresponds to something like a club with two levels of membership:
Basic Membership: To belong at all, you must be the father of exactly two children. It is easy to see that about 1/4 of members will have two boys.
Advanced Membership: You must also have a son who will join. It’s possible that not all boys will. But since GG fathers can’t advance, any one group that can (they are BB, BG, GB) represents a higher proportion of Advanced Members than they do of all members. That’s why the probability changes from 1/4 to 1/3 in Foshee’s method.
Now, suppose any given boy has only a probability P of being willing to join. A father of one boy who wants to advance has only P chance of getting to do so, while a father of two boys has a 2P-P^2 chance (for two sons minus the chance both will). Note that 2P-P^2>P, so the proportion of two-boy fathers increases more than one-boy fathers. And in fact, the three groups {BB,BG,GB} increase in the proportion 2P-P^2:P:P. This is not an “illusion,” or “astrology.” It is mathematical fact.
Now imagine a secret “Tuesday membership” in this club. You can figure out what that means. What Foshee’s method does, is to assume that P=1 at all levels, but that the effective P for Tuesday Members is 1/7 since only 1 in seven boys gets the chance to join at that level. What your method does is assume P=1 for advanced members, but is some complicated formula for Tuesday members (if they have a sister or a Tuesday Brother, P=1; otherwise, P=1/2). Foshee’s method is valid for his choice of P. Yours is not, because you do not treat P as an independent value).
BTW, mine corresponds to two kinds of Advanced Members, one for boys and one for girls, and a father can choose one but not both. And P is irrelevant. That way, the proportions are always 2:1:1:0 in the Boy level, and 0:1:1:2 in the Girl level.
One of the fascinating things about this topic is that the probability experts on the various threads cannot even agree on the answer to the simple question.
I could be wrong, but I think that Devlin, Bellos and Foshee are all in the 1/3 camp along with Jesper, but JeffJo and others are in the 1/2 camp. Matin Gardner apparently kept his options open.
JeffJo, as I’ve said before I really don’t care – you guys sort it out.
But just don’t try to tell me that if the answer is “X” to the simple question, then by revealing the child’s day of birth it goes to “Y”. As Jesper says – it’s an illusion.
.
There are two camps, but you mis-identified them. And the difference between them is the exact concept you are simultaneously rejecting and using incorrectly.
Devlin (look at the May article, not the April one), Gardner, Jesper, and I all say the problem can be ambiguous. When there is an option, the answer is 1/2 for both questions. When there isn’t, the answers are 1/3 and 13/27. The only disagreement among these people is when there is an option, not how it affects the answer. I say the option has to be assumed unless it is explicitly disallowed. Devlin and Jesper (apparently) think that it can be implied in certain contexts. Gardner was non-specific about when it applies.
The other camp seems to never have considered the option. At least, there is no evidence of it. They insist 1/3 is the only possible answer, and are quite wrong, as I outlined above. Essentially, they are making an assumption through ignorance (that means lack of knowledge, not stupidity) but are correct within that assumption. Once they accept the knowledge as a possibility, they always move into the other camp. That’s exactly what happen to both Gardner and Devlin. The others may be there as well, but as they don’t discuss the option we can’t know whether they never considered it, or if they just think it doesn’t apply.
You lie in between: You want to keep the answer from the camp who is wrong, by incorrectly applying the concept of the option. So you have the knowledge, but won’t accept what it means. And that is why you are wrong.
Oh, I forgot: according to Foshee, you are not “just revealing” the day of birth. This would be the option I keep talking about.
You are physically requiring the man to have a “Tuesday Boy” before he can be allowed to mention anything. Just like in your coin simile, you are required to PUT ANY MAN BACK IN THE SELECTION POOL if he does not have a boy born on a Tuesday. As soon as you examine that for what it means instead of ignoring it, you too will be in our camp.
JeffJo,
The coin simile is something I stole from Jesper.Talk to him about it.
You are all correct, kinda. :) It depends on whether Tuesday has been selected by the questioner, or by the subject.
If you ASK the mother this question, “Do you have exactly two cildren, at least one of whom is a boy, and is at least one boy born on a Tuesday”, and she answers yes, you now have a way to decide the likelihood she has two boys as being more than 50-50 because you have provided a criteria which is more easily met by having two boys, namely a boy born on Tuesday. YOU PICK THE DAY, any day will work.
If the mother VOLUNTEERS that she has a child born on Tuesday, you do NOT have any new criteria. She could as easily aswered Wednesday etc. You cannot now pretend that Tuesday is a filter of any kind, because you have allowed the sample to self-select it.
There is not a CORRELATION between Tuesday and two boys, any more than there is for any other day of the week. The reason this puzzle “works” in the first case is that you are using a specific day as a probe or filter. In the second case it fails because you are simply allowing the subject to select any answer.
This is very similar to the important hook in the 3-door question. If you had been given NO NEW INFO, then picking a new door is still 1/3 chance. The reason that puzzle works is that by being offered a choice ( as opposed to grabbing it) you get new info which changes the odds. Similarly, this puzzle only work if you PROBE for a specific day.
Which, as best I can read it, means that as presented above, the puzzle fails to have an “interesting” answer. When volunteered, the day of the week offers no real information into the probability.
Gary Foshee has fooled a lot of people, me too in the beginning.
The problem can not be solved with conditional probability, that’s a tool only for specialists.
Just Use common probability or Your intuition. That gives You four possibilities:
Boy-known + Boy,
Boy-known + Girl,
Boy + Boy-known,
Girl + Boy-known,
and of course 50% probability for two boys, also if Boy-known is born on a tuesday, is redhaired, has a canary or whatever.
I have tried to convince a danish blog, they still argue.
It seems that the problem is more difficult depending on Your education!
Place a coin random on a table showing tails.
It’s a coin made on a tuesday (or whatever).
Toss another coin, it lands randomly on the table.
What is the probability that both show tails?
I hope you agree in 1/2%.
Let the coins be children.
Let the first coin be a boy born on a tuesday.
Let the table be the possibilities young and (perhaps) elder child.
What is the probability that both children are boys?
I don’t see any difference between this and the
Gary Foshee puzzle.
My answer is 1/2%.
I wonder if Keith Devlin still think it’s 1/3!
1/2% = 1/2.
@Vagn
It sounds like you have been through the discussion already, so I am not going to convince you easily.
Since you seem certain that the result is always 1/2 no matter how the situation it set up, would you be willing to play this coin-flipping game with me?
*
a) We keep flipping two coins simultaneously.
b) If both coins are tails, we flip the coins again.
c) Otherwise, you give me $15 if there is one head, and I give you $20 if there are two heads.
If the probability is 1/2, you will be making money. If it’s 1/3, I will.
@Jesper
I Don’t want to discuss in english with a dane.
vgn.lsn@gmail.com
To everybody except Jesper:
Of course you have noticed that I did only toss one coin, similar to the fact that we know Foshee has (at least) one boy.
Hey Jesper and all others.
The solution is 1/2, Keith Devlin has admitted, that he is wrong.
He says in the revised “Devlin’s Angle” may 2010:
“Had I stated the problem as “Given that a man chosen at random has two children, at least one of which is a boy born on a Tuesday, what is the probability that he has two boys?” then the answer would be 13/27, as I derived.”
That is not correct either. He assumes we know that conditional (epistemic) probability should be used with 13/27 as correct answer, but normal probability still gives the answer 1/2. Every one of the chosen men has 1/2 probability, but 13/27 of the men has in fact two boys. A mathematician, who dosn’t see the difference, has not understood conditional (epistemic) probability at all.
Later he says:
“Now, people who like probability puzzles (and those of us who love to hate them, or do I mean hate to love them?) know about these complications, but we learn to read them a certain way. That way is very much part of the code of pure mathematics in general, and probability questions in particular. We dress them up as real life scenarios involving one or two people, usually the puzzle poser and her or his target, to personalize them, and avoid always talking about “randomly selected individuals from a population.” But it’s just part of a genre of dressing up mathematical questions in imaginary scenarios.”
Indeed it’s difficult to solve mathematic problems over there in the States, you have to guess what the teacher meant! This excuse is complete nonsense.
Mathematicians often uses the two boy question to demonstrate conditional probability, not always in a correct way. I still believe, that Gardner and Foshee knew the right answer from the beginning.
The Foshee question: “I have two children. One is a boy born on a Tuesday. What is the probability I have two boys?” is not at all ambiguous. He has a boy, that’s a fact, we only have to guess the gender of his second child, result 1/2.
Only 13/27 of men with two children, of which one is a boy born on a Tuesday, has two boys, but that’s not the question.
As stated in the book “Oxford Users’ Guide to Mathematics” from “Oxford University Press 2004”:
“It is important to make a clear distinction between normal probabilities and conditional probabilities.”
@Vagn
First, this is a conditional probability problem. The “normal” probability of a two-boy family, the one Oxford means, is 1/4. As is the “normal” probability for any of the other three possible combinations. A conditional probability is when you learn that some combinations could not have happened in a specific case, and you have to renormalize the remaining possibilities so that they add up to 1. We are using conditional probability when we say that the GG case, and maybe some BG or GB cases, are no longer possible. We “renormalize” the 1/4 “normal” probability by dividing it by the total probability of what remains possible, either 3/4 or 1/2, and thus get either 1/3 or 1/2.
But that’s not what I came here to tell you about. I’ve thought of a different way place the emphasis when explaining this controversy. The issue is how you associate probability with proportion.
By proportion, I mean the fraction of a whole that has some property. Of all the two child families in the world that include a boy born on Tuesday, the fraction that have two boys is 13/27. This is an indisputable, arithmetical fact. It is as easy to determine as counting beans – in fact, you could do it that way. Get 196 beans, and write each possible combination of two of the 14 “types” of children on individual beans; one “type” on each side. 27 of them will have “Tuesday Boy” written on them somewhere, and 13 of those will have “boy” written twice.
Proportion can be used to determine probability, but only if you get the right “whole” to measure it against. If you put just those 27 beans in a jar and draw one (or equivalently, put all of them in, and draw until you get one that says “Tuesday Boy”), then the probability, that the one you drew says “boy” twice, is equal to the proportion I just calculated. It is the correct probability because I contrived the situation so that the “whole” was a number of beans.
But if you just draw a bean and read one side, and it happens to say “Tuesday Boy,” then the probability the other side says “boy” is 1/2. That’s because the “whole” I need to use now, is the number of *sides* that say “Tuesday Boy.” Not the number of beans that say it on either side. “Tuesday Boy” was written on 28 sides (one bean has it twice), and 14 of those say “boy” on the other side of the same bean.
The issue is, what “whole” does Gary Foshee measure himself against? That isn’t clear, and both answers are still possible. I don’t know if you know the history of this problem, so here’s a brief one: in 1959 Martin Gardner asked the question “Mr. Smith has two children. At least one of them is a boy. What is the probability that both children are boys?” He first said the answer was 1/3, but latter admitted the puzzle was not clear enough and it could be 1/3 or 1/2.
Now, suppose a man I will call GF wants to re-introduce this puzzle (without Tuesday) at a conference honoring Gardner. He notices that he has two children, so he can use his own family as an example. There are four possible GFs, call them GF1, GF2, GF3, and GF4, for the four family types BB, BG, GB, and GG, respectively.
Wanting to match Gardner’s version of the puzzle as closely as possible, GF1, GF2, and GF3 will say “I have two children, and at least one is a boy” and ask for the probability of two boys. But GF4 can’t – he, and he alone, will say “I have two children, and at least one is a girl” and ask for the probability of two girls. As you can clearly see by using proportions, the correct answers to the two questions are 1/3 and 1/1, respectively.
Just to be clear, I said it is a certainty that any GF who says “at least one girl” has two girls. That is a necessary side effect of the answer to the “boy” version being 1/3. But it is an entirely plausible happenstance for GF, since he is trying to match Gardner’s question and so had a prior constraint. It is not, however, an acceptable answer to a puzzle. The two symmetric forms have to have the same answer, and that can only be 1/2. It isn’t because 1/3 can’t be right, it is because assuming a prior constraint means it has to be in place before the random GF is chosen, so it affects GF4 differently. If the puzzle doesn’t explicitly mention a prior constraint, we can’t assume it.
And Keith Devlin did not say he was wrong, he only admitted the ambiguity. With the assumption of prior constraint that he makes (which I disagree is implied by using the words “given that”), the correct answer is 13/27, just like the correct answer to GF1, GF2, or GF3’s question is 1/3. But the same prior constraint also means that if he had said “Friday Boy,” the answer could not be 13/27, which is why it is unacceptable.
JeffJo Says:
July 7th, 2010 at 11:23
Oh, I forgot: according to Foshee, you are not “just revealing” the day of birth. This would be the option I keep talking about.
You are physically requiring the man to have a “Tuesday Boy” before he can be allowed to mention anything. Just like in your coin simile, you are required to PUT ANY MAN BACK IN THE SELECTION POOL if he does not have a boy born on a Tuesday. As soon as you examine that for what it means instead of ignoring it, you too will be in our camp.
@JeffJo
How can you say that? You seek a person in a “the selection pool”, but Foshee just said, that he had a boy born on a Tuesday. If you sought another person with a son born on a Tuesday, then you had to seek in “the selection pool”.
I have nothing more to say to you.
@Vagn
I didn’t say Gary Foshee’s assumptions are good, I said that his answer is correct based on his assumptions.
Also, you don’t seem to understand isomorphism. That’s where you take one probability problem and transform it into an equivalent one that is easier to visualize. Asking the members of an audience to raise their hands if they have two children including at least one boy is equivalent to “drawing” people from a selection pool, checking to see if they have two children including at least one boy, and re-drawing if they don’t. Both methods will successfully identify 3/4 of the group as meeting the requirements, and 1/3 of those identified will have two boys. And yes, it changes to 13/27 if you add “Tuesday.”
Where I don’t agree with Gary Foshee, and do agree with you, is that his question does not uniquely identify either of those methods as the correct isomorphism for his question. There is another set, which Ron calls “reveal,” where one specific child is somehow identified as a boy. Whether it is the “older,” or you met him, or the parent merely tells you that one child just joined the Boy Scouts, it is clear that “boy” refers to a specific child independent of his sibling. Then, the answer is 1/2 regardless of any other information.
Where I disagree with you, is that the question is ambiguous; any of the interpretations I have described are *possible*. If Gary Foshee actually has two boys who were born on Tuesday, his statement is not “clearly” about either one of them. In probability, if you can’t find a reason an outcome is impossible, you must still treat it as possible. And this Gary Foshee could be talking about either, so the first two isomorphisms woud be correct.
But ultimately, I said that between the different interpretations that are possible, without clarification of some kind the ones that produce 1/2 are plausible while the ones that produce 1/3 (or 13/27) are not. In the end, I agree with you, just not as strongly. So why do should refuse to talk to me?
To Keith Devlin
Your new formulation:
“Given that a man chosen at random has two children, at least one of which is a boy born on a Tuesday, what is the probability that he has two boys?”
is very ambiguous. If you choose a man random and then tell us etc., then the answer could be 1/2. This is a correct formulation:
“Given that a man chosen at random – among those who – has two children, at least one of which is a boy born on a Tuesday, what is the probability that he has two boys?”.
In this case 1/2 would be a wrong answer.
I agree 100%; in fact, I said the same thing before. I even emailed Devlin suggesting that very change. He did not respond.
The “code” that Devlin talks about is not the use of the word “given,” it is the fact that in probability what is “given” to us is supposed to be a set, not a description of an individual element of the set. So while P(A|B) is usually read as “The probability of A given B,” what it really means is “The probability that an outcome in set A occurred, given that the outcome was constrained to set B.”
What the English statement “Given that a random man’s family has property X” establishes, is just a necessary condition for an outcome to belong to some set B. We know that all families in B have X, but not whether all families that have X are in B. To fully define B, we also need a sufficient condition.
I think this will be my last comment.
1. “I have two children. One is a boy (born on a Tuesday). What is the probability I have two boys?”
This problem is not ambiguous at all. All fathers have 1/2 probability of two children of the same sex, no matter what we know about one child. If the problem has to be solved with conditional probability it must be specified explicitly.
2. “A man says: “I have two children. One is a boy (born on a Tuesday).” What is the probability he has two boys?”.
This is very ambiguous. Does it relate to this man or average? The solving method must be specified, else it’s an invalid mathematic problem.
3. “What is the probability of finding a man with two boys among those with two children, of which one is a boy (born on a Tuesday)?”
This problem can only be solved with conditional probability, result 1/3 (13/27).
@JeffJo
Sorry, I didn’t notice “according to Foshee”, I was wrong.
Ps. It’s a bit difficult for me to discuss in English, I make frequent use of my dictionary. My native language is Danish.
Vagn, you forget that whether a probability is conditional, and what the condition is, depends on point of view.
To you, the speaker of #1, it is not a conditional probability. Or a probability at all, for that matter. That’s because you know the genders for a fact.
When I hear you say what you did in #1, from my POV it is no different from #2. In fact, it is exactly your POV in #2. It is a conditional probability. Both are ambiguous, but the best answer is 1/2 because anything else requires assuming a bias of some sort exists.
Say that I draw one card, and it is the Queen of Hearts. I tell Ann it is red, Bob it is a face card (TJQKA), Carl that it is a Heart, and Dee that it is a Queen. If I ask “what is the probability it is the Queen of Hearts,” their correct answers are 1/26, 1/20, 1/13, and 1/4.
I cannot answer that question, because to me it is not random at all – “probability” is not a property I can associate with a known value. I can answer “What was the probability, before I drew it, that it would be the Queen of Hearts?” That is 1/52.
@JeffJo
Ask your grandma:
“I have two children. One is a boy (born on a Tuesday). What is my chance of having two boys?”
I am sure you will get the right answer, 1/2. The card is drawn. It dosn’t matter if the son is first or second born.
Read your book about conditional probability once more, you haven’t understood it at all. This discussion is totally waste of time.
Good-bye.
JeffJo,
Doesn’t it make you yearn for the good old days when you had someone reasonable and tolerant (like me) to debate with!
I have studiet the blog a little more. I don’t understand how a mathematic problem can be ambiguous? For me “ambiguous = wrong”, am I wrong in that? As I see it, that’s the entire problem.
@Jesper
Let’s play the coin-flipping game:
a) We keep flipping two coins simultaneously.
b) If both coins are tails, I win, you give me $20.
c) Otherwise, I give you $15 if there is one head, and you give me $20 if there are two heads.
If the probability is 1/3, you will be making money. If it’s 1/2, I will.
Will you play?
Did you ever see a croupier cancel a game because he didn’t like the result? Your game exposes your lack of understanding.
JeffJo said:
1. “A problem statement can be misleading if it is described as an example, because an example only describes posterior events. That is where we need to get the answer from, but their probabilities can never be calculated directly. They must be calculated from the prior probabilities. So we must extrapolate what the condition C was before it was applied, not after. Then, the posterior probability of any event E is the prior probability of E and C happening together, divided by the prior probability of C happening. This is a definition.”
and:
2. “There is no such thing as “the math puzzle genre,” that is a rationalization used to cover an assumption that is incorrect.”
I think he contradicts himself. First he defines what I would call “the math puzzle genre”, later he denies that it exists!
Vagn: “I don’t understand how a mathematic problem can be ambiguous? For me ‘ambiguous = wrong’, am I wrong in that?”
Ambiguous means “can be interpreted in more than one way.” For example: I just placed two coins, face up, on the desk in front of me, making sure at least one is heads. What is the probability both are heads? Would you bet $1, to win $5, on this question? How often?
When the man says “at least one is a boy,” does that mean he choose a child and told us that child’s gender? Then the answer is 1/2. Or does it mean he choose a gender, and agreed that he had at least one matching child? Then the probability is 1/3. Setting reasonableness aside, either interpretation is possible, so the question is ambiguous.
Let’s try a slightly different coin-flipping game; Here’s a demonstration (and yes, I am actually doing this) of my game:
1) I flip two coins so you can’t see.
2) I tell you “At least one landed on heads.”
3) You can bet $1 on whether the two coins show the same side, or different.
If you win a bet that they are the same, I will pay you back $2.40. So you will win an average of $0.20 a game if the probability is 1/2, but I win an average of $0.20 if the probability is 1/3.
If you win a bet that they are different, I will pay you back $1.71. So you will win an average of $0.14 a game if the probability they are different is 2/3 (corresponding to “1/3” for “the same”), but I win an average of just over $0.14 if the probability is 1/2.
(By the way, “the same” won.)
I offer to repeat this game, according to a fixed procedure, as often as you want to play it. But only if you will as you bet the same way you did there each time. If you choose to bet on “different,” the procedure is that I tell you what came up each flip, and I win $0.14. If you bet on “the same,” the procedure is I reflip anytime I get two tails so that I can say “heads” as in the example, and I will win $0.20. In either case, did I contradict the example? I am not a croupier; but I might be someone who is looking for a heads, not looking for every result.
Now, I agree the first is not a good interpretation. All I’m saying is that it is a *possible* interpretation. And the only valid points of discussion here are why it is or isn’t, and why some people assume it is.
Vagn: “I think he contradicts himself. First he defines what I would call ‘the math puzzle genre,’ later he denies that it exists!”
The definition was for a conditional probability, and has nothing (directly) to do with puzzles. When you know an outcome was constrained, somehow, to event C, then the conditional probability (sometimes called posterior probability) of event E IS DEFINED TO BE the original probability of both events E and C happing at the same time, divided by the original probability of event C happening regardless of E.
So, if E is “family has two boys,” and C is “family has at least one boy,” then P(E&C)=1/4, P(C)=3/4, and P(E|C)=(1/4)/(3/4)=1/3. People get this answer, probably, by placing too much emphasis on the language used, and not recognizing that “Event C” is a set of possible outcomes, not a description of one outcome.
But if C is “Father chooses ‘at least one boy’ randomly from all of {‘at least one boy’, ‘at least one girl’} that apply,” which seems more likely to describe the set, then P(E&C)=1/4, P(C)=1/2, and P(E|C)=(1/4)/(2/4)=1/2.
But you have shown yourself to be someone who has little knowledge of the actual mathematics of probability, and little desire to discuss it. Your inability to grasp what others say goes beyond a language barrier; you seem to actively seek ways to misunderstand (or at least, you fail to try to understand when it is easier to misunderstand by reading only superficially). So unless that changes, I now have nothing more to say to you.
JeffJo,
That told him! We Europeans know that these Danes can be spiky and rude (unlike their nice Swedish neighbours over the Oresund).
Some say that some of their rudeness has been inherited, via the Viking invasions, by the British.
Anyone who does say that is an idiot.
@JeffJo
Apparently you have lots of time. Of course I know what ambiguous means, please don’t try to teach me everything I know already.
You say: ““Event C” is a set of possible outcomes, not a description of one outcome.”. That’s exactly the question, Foshee’s question is one outcome, not a set.
Your coin game is ridiculous. Remember I win if the result is two tails.
One more time for JeffJo:
For me an ambiguous mathematic question is an invalid mathematic question.
I really hope you have nothing more to say to me.
What is the probability he has twins?
this would make the day the most important fact in his grammar
Answer: It’s a Girl about 37 to 39 years old…. I still have the Coke bottle given to me about 1975 by Gary. I also have a box Gary made for my work, in a Radio Car…. Gary love to go on ride-a-longs. Gary is an extraordinary man and puzzle enthusiasts.. I hope this gets back to him in so way, been a long time
Dick Martin